近似値から真の値の範囲を求める 「四捨五入」というものがありますね。 何のために四捨五入をするのか? 概数を出すためですね。 では、何のために概数を出すのか? まずはそちらからご説明いたします! ! 数量を測る際に、桁数が多かっ真 の 値 に 近 い値をいい、測定や近似計算によって得られる。 たとえば15℃の空気中の音の速さの近似値は毎秒340メートル、分数1/3の近似値は033、 円周率 の近似値は314などである。誤差=近似値-真の値 有効数字 近似値を表す数で、意味のある数字のこと。 ※どこまでが有効数字であるかはっきりさせたいとき、 (整数部分が1けたの数)×(10の累乗)の形で表すことがある。

中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier
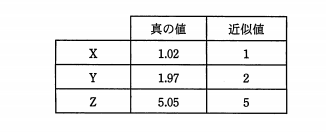
相対誤差 近似値 真の値
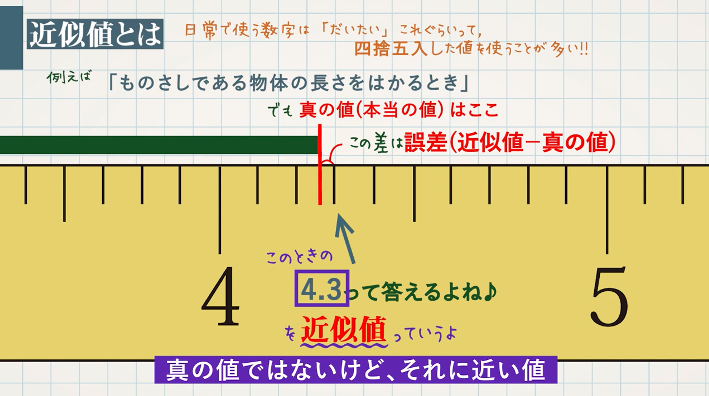
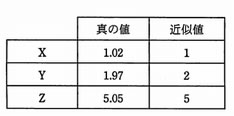
相対誤差 近似値 真の値-平成23年 春期 基本情報技術者 午前 問02 問02 相対誤差 三つの実数 X ~ Z とそれぞれの近似値が次の場合,相対誤差の小さい順に並べたものはどれか。 真の値 近似値 X 102 1 Y図の緑の長さは 43 と答えますが、真の値(本当の値)は ・ ・ ・ 428 ・ ・ ・ となります。 このときの 43 を 近似値 といいます。



名城大学 小澤研究室
測定値(近似値)として, 34g を得たとき, 有効数字(信頼できる数字)は2けたで,3と4(1gの位まで信頼できるから)→ 34×10と表す (整数部分が1けたの数)×(10の累乗) の形で 真の値は, 335g以上345g未満(01の位を四捨五入して得られたから)誤差 近似値と真の値との差。 有効数字 近似値の表す数のうち,信頼できる 数字。有効数字をはっきりさせるには,整数部 分が1けたの小数と 10 の累乗の積の形で表す。 例 mmの位まで測定した 250 250×102 7資料の活用 学習のポイント 相対度数や代表値を長さや重さの測定値は、およその数値なので、真の値とは異なります。このように、真の値とは異なるが、それに近い値を 近似値 といいます。また、近似値と真の値との差を誤差といいます。一方、体重をはかるとき、 \(\color{crimson}{a)\;485kg \quad b)\;4850kg}\)と測定する \(2\) つの体重計があ
誤差 = 近似値 - 真の値 なので、 誤差 = 500 - 492 = 8 答 8人 (3)家から駅までの距離2850mを3000m と表した。 誤差 = 近似値 - 真の値 なので、 誤差 = 3000- 2850 = 150 答 150m 例題2 小数第1位を四捨五入して30になる数χ 目次000 真の値・近似値624 有効数字 チャンネル紹介授業 仁塾へようこそ。このチャンネルでは、学校では教えてくれない"問題を解く技"を近似値の真の値の範囲を求 める。 有効数字の意味を知り、近似 値を(整数部分が1けたの数) ×(10の累乗)の形に表す。 〇 〇 ・近似値、誤差、有効数字の意味と近似値の表し方 を理解している。〔観察、発言、ノート〕 ・真の値の範囲を不等号を使って
1年以上前 悠ョ_° (年5月12日に垢変します) 真の値とはなんですか? 初めて聞きました笑 次の問いに答えなさい。 (1) あるものの長さをはかったところ, 87cmになった。 真の な範囲にあると考えられるか, 不等号を使って表しなさい。真の値をそれぞれaとして,その 範囲を不等号を用いてそれぞれ表しなさい。 (1)96g (2)176m 3次の値を有効数字が3けたの近似値とするとき,有効数字がはっきりわかる形で表しなさい。近似値と真の値の差を誤差という。 誤差=近似値ー真の値 四捨五入 1245を小数第1位で四捨五入すると12,小数第2位で四捨五入すると125である。 どのけたを四捨五入するかによって誤差や真の値の範囲が異なる。 例 小数第1位を四捨五入して25になる数aに




近似値 有効数字 無料で使える中学学習プリント
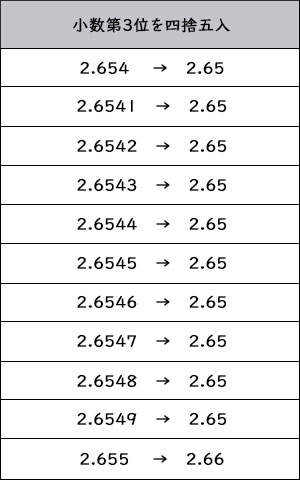



中学校1年生数学 近似値 長野地区 Itto個別指導学院 長野市の学習塾
近似値とは? 近似値とは、真の値に近い値のことで、次のようなときに真の値の代わりに使用されます。 真の値を求めるのが難しい 「非常に複雑な関数について考えたい」「複数の要因が絡み合う物理現象を扱いたい」ときなど、限られたリソース(人の頭脳、コンピュータ)では正確を得る. √ 5 の近似値として 9 4 を考えたが,これを使うと √ 5 = 4 √ 16 81 ·5 = 4 √ 1−1 81 が得られて, √ 5 の近似値 9 4(1− 1 162) = 161 72 = ···を得る.実際の値はこれより大きいが誤差は9 4 1 4 1 812真の値10(度)との誤差は、約 0001(度) これは、10メートル進むと1cmの開きがでるぐらい、100メートル進むと10cmの開きができるぐらいの差です。 この誤差をもっと小さくする場合は、さらに、7次近似、9次近似を計算することになります。
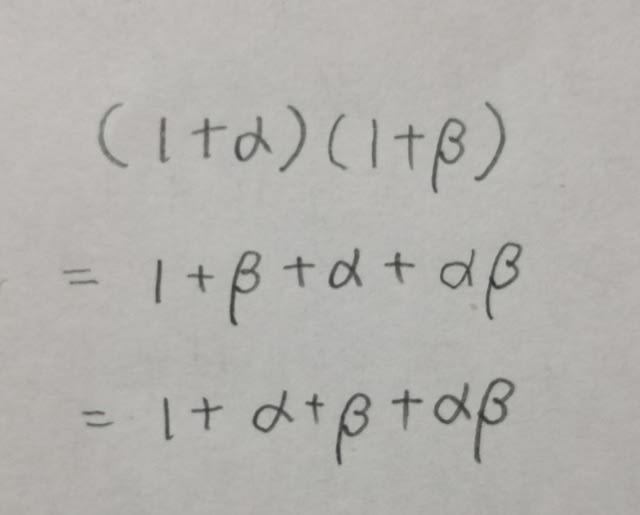



15の続き 近似値計算 公務員試験知能 教員採用試験数学解説




中1 数学 資料の整理7 近似値とは 13分 Youtube
近似値 真の値 という計算をすることで、真の値からどれだけずれているかがわかります。 5 499 = 001 だったら、真の値499より001だけ大きくなっているわけです。つまり、実際には001の引き算があったものを近似によって削ってしまったわけです。 誤差と有効数字、近似値の表し方の問題です。高校の理科でも使う分野なので、教科書でしっかり意味を確認してから問題に取り組んでください。誤差とは、真の値と近似値との間にある違い、つまり、誤差=近似値-真の値です。例)測定値 505kg 真の値 502kg のとき 505kgー502kg=03kgが誤差2平方根 平方根の値を求めよう 4 3 年 組 氏名 1 の値を求めるのに,次のような2つの方法で解きました。 q にあてはまる数を求めよう。(近似値法) 60 2=,70=,802= だから, < < 次に,71 2=,72=, 732=,742== w 開平法(例)




近似による誤差 Wikipedia



The 7th Week J
測定値(近似値)として, 34g を得たとき, 有効数字(信頼できる数字)は2けたで,3と4(1gの位まで信頼できるから)→ 34×10 と表す (整数部分が1けたの数)×(10の累乗) の形で 真の値は, 335g以上345g未満(01の位を四捨五⼊して得られたから)真の値は なお,ここでは小数第4位を切り捨ててあり, 最終的に有効数字2桁で計算結果とした。高校の 教育現場では有効数字2桁が多いからである。 4問題点と改善方法 (1)誤差の確認 真の値とこの近似式に基づいた近似値を比較し てみたのが別表1である。ある数 a の小数第1位を四捨五入した近似値が18になった。(1)a の範囲を不等号をつかって表しなさい。(2)誤差の絶対値はいくら以下であると




近似値と有効数字 教遊者




08 号 電力値真値からデシベル値への変換方式 Astamuse
出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 0443 UTC 版) 相対誤差の利用 相対誤差は、全く異なる大きさの値に対する近似値の精度を比較する場合にしばしば使われる。 例を挙げると、真の値が1000であるのに対し近似値を1003と与える場合と、真の値がであるときに近似値測定値(近似値)として, 34g を得たとき, 有効数字(信頼できる数字)は2けたで,3と4(1gの位まで信頼できるから)→ 34×10と表す (整数部分が1けたの数)×(10の累乗) の形で 真の値は,335g以上345g未満(01の位を四捨五入して得られたから)最頻値(モード) 真の値に近い値のことを何というか。 近似値 近似値から真の値をひいた差をのことを何というか。 誤差 個々の資料の値の合計を資料の総数でわった値のことを何というか。 平均値 平均値を求める式は?



2
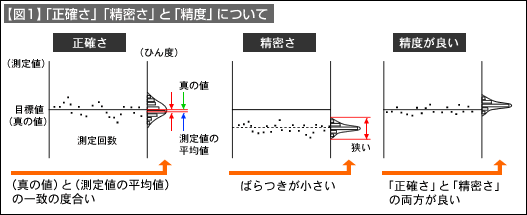



精密測定における精度と誤差の関係 Lca ローコストオートメーションと計測 技術情報 Misumi Vona ミスミ
近似値と有効数字 本時の目標 近似値、真の値、誤差の意味を理解する。 有効数字の意味と表し方を理解し、測定値を有効数字で表すことができる。 ※問題は、略案で創る中学校数学科の授業より引用近似による誤差は2つのグラフの差であり、 x の値が0より大きくなるほど誤差も大きくなっている。 近似による誤差 (きんじによるごさ)とは、 真の値 と 近似値 の差のことである。近似値と有効数字(2) 中1数学 資料の整理と活用 1ある学校の生徒数 1161人の近似値として10人を用いるとき,誤差を答えなさい。 (誤差)=(近似値)-(真の値) より,10-1161 = 39 答え 39人 (1) 134cm (2) 230kg 答え (1) 範囲 1335cm ≦ 𝑎< 1345cm 誤差 05cm 以下




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier
近似値 177 近似値測定値や四捨五入して得られた値のように、真の値ではないが、それに近い 値のこと。 誤 差近似値から真の値をひいた差のこと。 (誤差)=(近似値)-(真の値) ある数aの小数第1位を四捨五入したら7になった。真値 の用例・例文集 この値のことを誤差理論において 真の値または真値 と呼んでいる。ここで言う「真値」とは「定義に矛盾しない観測量の値 」のことである。計算する際は数を区間に置き換えて計算し、真値を含む区間を結果として出力する。キーワード真の値,近似値,誤差,測定値 Ⅰ.問題の所在 現行の学習指導要領に沿った中学校数学科では, 中学校 1 年生で近似値の指導がされていて,近似値 を「測定して得られた値などのように真の値
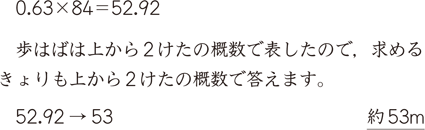



測定値と有効数字 算数用語集



2




中学校数学自宅学習1年 資料の活用 近似値と有効数字



名城大学 小澤研究室



1 01 1 3 の近似値を F X 1 X 1 3 のx 0 Yahoo 知恵袋




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中1数学 近似値 練習編 映像授業のtry It トライイット




近似値 有効数字 無料で使える中学学習プリント




イメージでわかる冴子先生の高校数学 近似式編 数学はこちら 漫画で表してます Manabi100




中3数学 真の値 近似値 有効数字 Youtube




近似値 近似式とは 公式や求め方 テイラー展開 マクローリン展開も 受験辞典




資料の整理について 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生




中1数学 近似値 練習編 映像授業のtry It トライイット




平方根 清水塾



1




近似値は 4 8真の値って何になりますか Clear




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1



Researchmap Jp A509 Presentations Attachment File Pdf




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 近似値と誤差の求め方の定期テスト予想問題 Pikuu




P値を使わないフィットネステストの評価法



近似値と有効数字 教遊者




微分積分学 基礎数学 7回目




近似値と有効数字 教遊者



The 7th Week J




1枚目と二枚目の真の値の求め方聞かれてるのは一緒なのに解き方ちがうとおもんですが Clear



基本情報技術者試験過去問解説 平成23年春 問2



近似値 近似式とは 公式や求め方 テイラー展開 マクローリン展開も 受験辞典




中1数学 近似値と誤差 Youtube



Http Www Edu C Pref Miyagi Jp Tangen Math Jun1 Math Comment 26hop Pdf



2




1枚目と二枚目の真の値の求め方聞かれてるのは一緒なのに解き方ちがうとおもんですが Clear



Www Pref Osaka Lg Jp Attach 6629 Jmw 1d7 5 Pdf




中1 数学 近似値と有効数字 中学生 数学のノート Clear




08 号 電力値真値からデシベル値への変換方式 Astamuse




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




誤差と相対誤差 ライブラリ Opeo 折川技術士事務所



Www1 Iwate School Jp Action Common Download Main Upload Id 1258




近似値と有効数字の求め方とは どちらも情報の 度が大事 遊ぶ数学




中1 数学 近似値と有効数字 中学生 数学のノート Clear




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学1年の数学 動画 近似値の問題 19ch
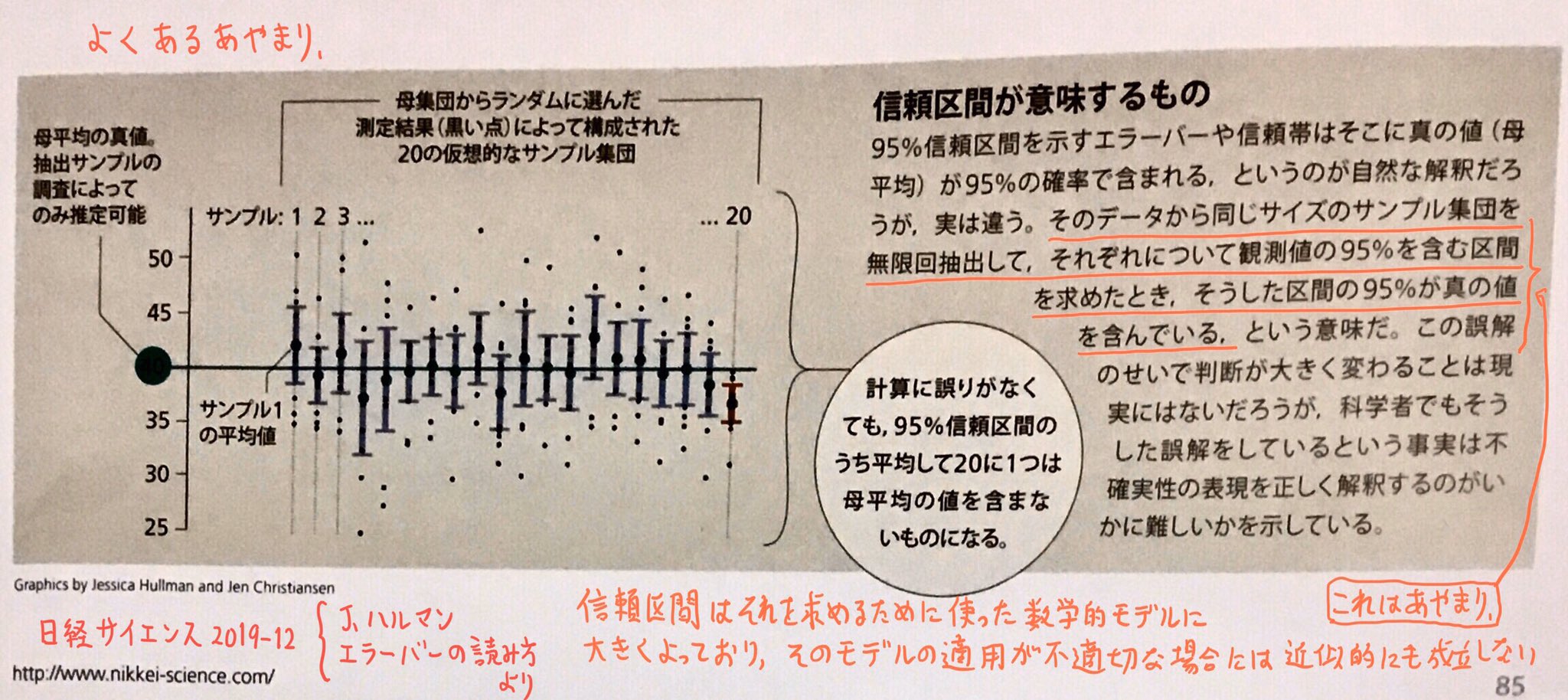



黒木玄 Gen Kuroki 統計 信頼区間について説明するときに 確率 という用語を避ける習慣はおそらく世紀にあったフィッシャーさん達によるくだらない論争 黒歴史 に由来しているのだと思う 真の値は未知だが固定されており 信頼区間がサンプルの無作為




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月
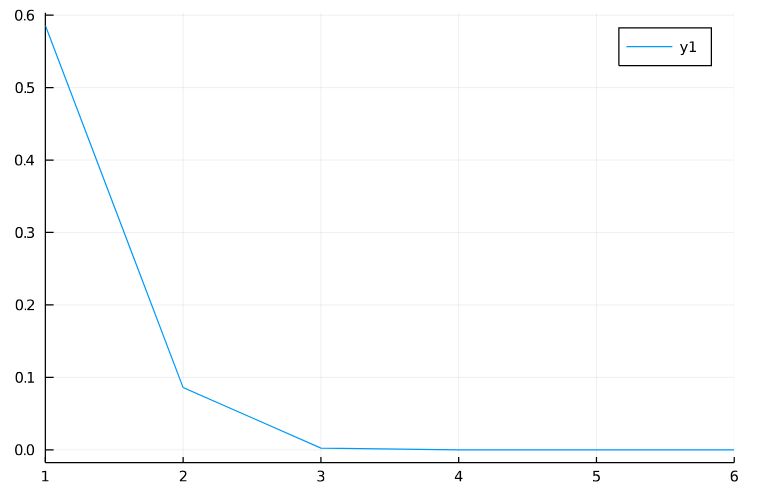



ニュートン法によってルート 円周率の近似値を求めてみよう 趣味の大学数学




世界一わかりやすい数学問題集中1 7章 資料の活用



近似値 近似式とは 公式や求め方 テイラー展開 マクローリン展開も 受験辞典




10g 10g D 1 10 1 Left Descubre Como Resolverlo En Qanda




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



回帰分析への測定誤差の影響



2



2




ルート3の近似値の求め方4パターン 数学の星



次の数はいずれも少数第二位を四捨五入して得られた近似値です 真の値はどの範囲に Yahoo 知恵袋



1



Www City Hadano Kanagawa Jp Www Contents Simple 421 Pdf
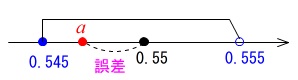



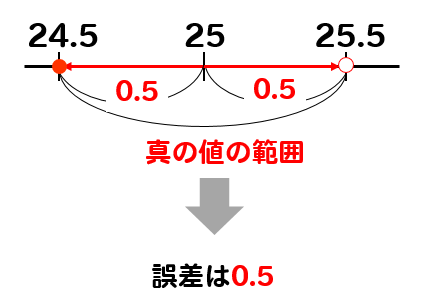
近似値とは 誤差の大きさと真の値の範囲の表し方 中1資料の活用




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中1数学 有効数字 近似値と誤差の要点と定期テスト対策問題 Examee



2
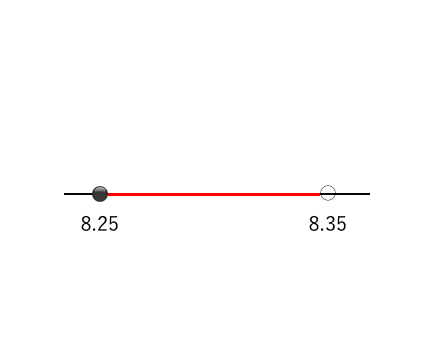



近似値の問題 苦手な数学を簡単に




33 4 1 Zz 2 Ee Descubre Como Resolverlo En Qanda




中学1年生 資料 近似値 誤差 有効数字 用語
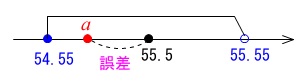



近似値とは 誤差の大きさと真の値の範囲の表し方 中1資料の活用




中3数学 近似値 真の値と誤差 Youtube



Http On Study Jp Math 1 51 Pdf



中学3年生真の値と近似値についての問題です ある数aの少数 Yahoo 知恵袋




Tossランド 近似値と有効数字 オンライン授業対応




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平均値の求め方 近似値 真の値 誤差の求め方 中学1年数学 資料の分析と活用




中1 数学 中1 近似値 Youtube



スマホ 必ず受かる情報処理技術者試験 平成23年度特別 基本情報技術者 解答




中1数学 近似値 練習編 映像授業のtry It トライイット



無料 中1数学 基本解説 問題プリント 資料の活用2 近似値 145




第一回



第2章10平方根 平方根の近似値 フロントエンドなブログ



平均値の求め方 近似値 真の値 誤差の求め方 中学1年数学 資料の分析と活用




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




中1数学 近似値と誤差のポイントと練習問題 中学生勉強サイトあかね先生




中3数学 近似値 真の値と誤差 Youtube



2




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



1



2




A Descubre Como Resolverlo En Qanda




中1数学 近似値 練習編 映像授業のtry It トライイット




08 号 電力値真値からデシベル値への変換方式 Astamuse




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier



3 13 測定値とは 神栖市立神栖第二中学校
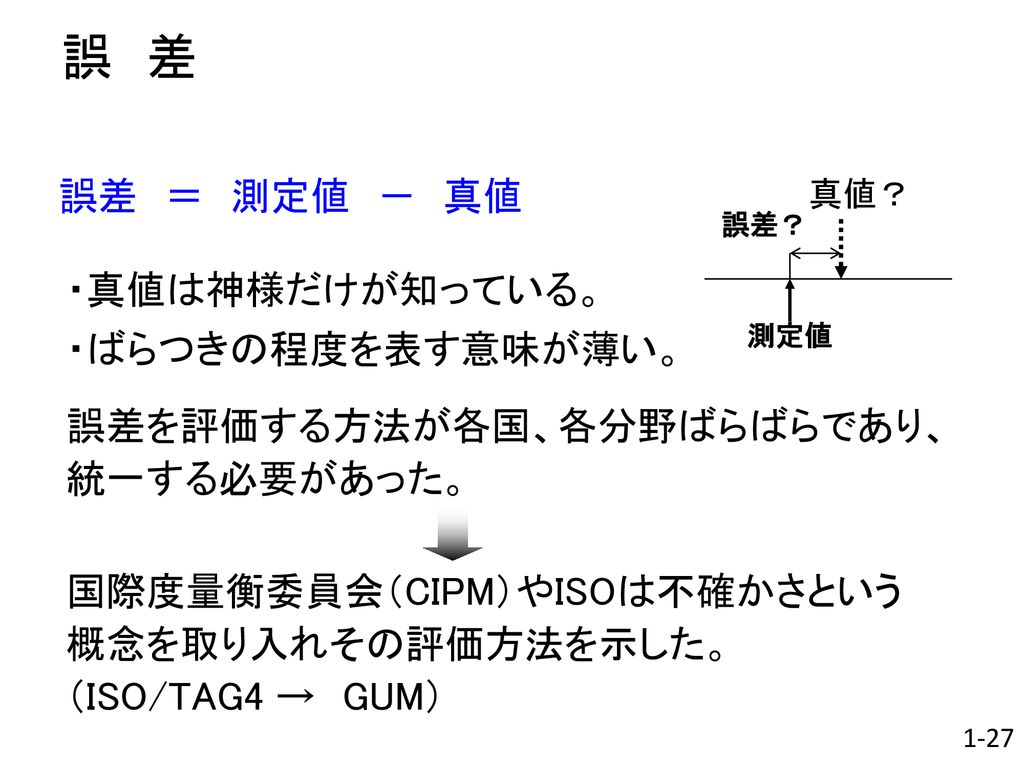



誤 差 誤差 測定値 真値 真値は神様だけが知っている ばらつきの程度を表す意味が薄い Ppt Download



0 件のコメント:
コメントを投稿