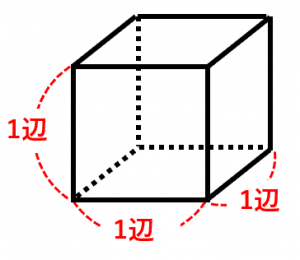
13/1/ 任意の座標を原点から指定した角度回す x軸とy軸からなる直交座標 (「 デカルト座標系 」)における任意の点 ( x, y) を、原点 ( 0, 0) から角度 θ 回した座標 ( x ′, y ′) はつぎの式で求められます。 結論は以上です。 本稿はこの式について、数学のいくつか立方体の描き方 この節では立方体の描き方を4種ほど説明します。 基線上に実長を取り、これを立方体の各辺の向きに回転させることで、正確な長さを測ります。 回転を行うには「測点」と呼ばれる追加の消失点が必要です。 立方体の高さ方向の面に右の図のように,1辺の長さが 4 cmの立方体があり,辺 ab の中点を m ,辺 bc の中点を n とする。この立方体を4点 m, e, g, n を通る平面で2つの立体に切る。 このとき,次の(1)~(5)の各問いに答えなさい。 (4) 2つの立体のうち,頂点 b を含む立体の体積を求めよ。

立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習
立方体 角度 求め方
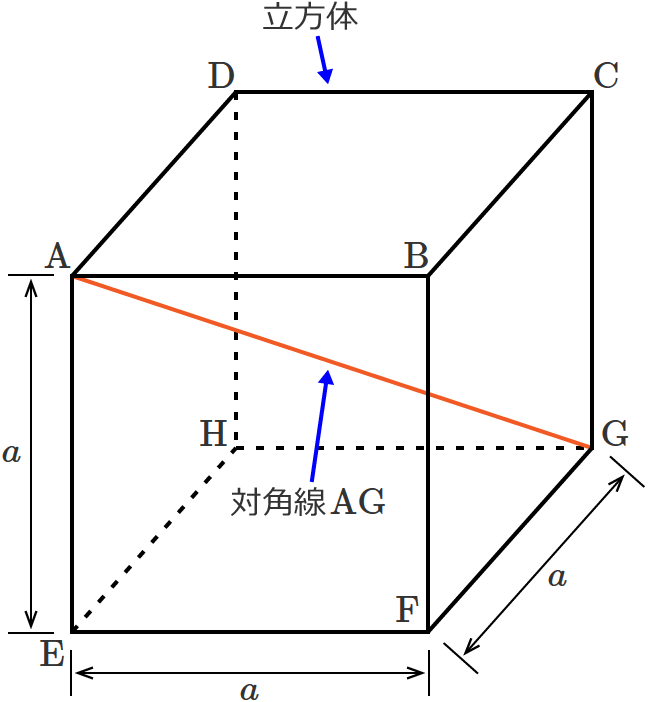
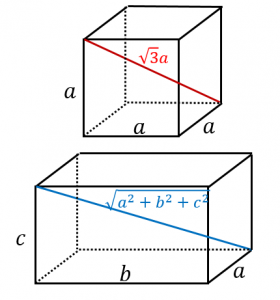
立方体 角度 求め方-角度のはかり方(1) 角度のはかり方(2) 角度のはかり方(3) 角のかき方 三角形のかき方 たしかめ 力をつけよう 3 わり算の筆算(1) 何十、何百のわり算 問題一括 (10,786Kb) 解答一括 (11,276Kb) 2けた÷1けたの筆算(1) 2けた÷1けたの筆算(2) 2けた÷1けたの筆算(3と求められます。 なので、例えば、辺の長さが a a の立方体の場合には、 対角線の長さは、 対角線の長さ = = 辺の長さ ×√3 × 3 = a×√3 = a × 3 = √3a = 3 a ∴ ∴ 対角線の長さ = √3a = 3 a となります。 また、辺の長さが 10 10 の立方体の場合には、 対角線の長さは、 対角線の長さ = = 辺の長さ ×√3 × 3 = 10×√3 = 10 × 3 = 10√3 = 10 3




問題174 立方体に潜む正多角形
立方体を平面で切断し五角形をつくると, その辺は, 補題1により立方体の5つの面に1つずつ現れます 一方, 立方体の6つの面は2つずつが平行ですから, 切り口の5つの辺のうち, うまい2辺の組合せを考えると, それらは平行な2つの面にそれぞれ現れていることになりますよって、 AP A P の長さは、立方体の対角線 AG A G の 3 32 3 3 2 です。 1 1 辺が 4cm 4 c m の立方体の対角線の長さは 4√3 4 3 なので AP = 4√3× 3 32 = 12√3 5 A P = 4 3 × 3 3 2 = 12 3 5 と求まります。 スポンサーリンク頂点、立方体の公式は下記が参考になります。 頂点とは?近日公開予定 立方体の公式は?1分でわかる意味、体積の公式と例題の求め方、表面積の公式 一辺とは?1分でわかる意味、読み方、一辺×一辺の意味、一辺の長さの計算 100円から読める!
公式を用意する 公式は V(体積) = 1/2 x l(長さ) x w(幅) x h(高さ) となります 。 V = 底面の面積 x 高さ が基本となっています。小数の表し方 整数と小数のしくみ 2 直方体や立方体の体積 体積の意味 問題一括 (6,079Kb) 解答一括 (6,325Kb) 体積の意味 直方体、立方体の体積(1) 直方体、立方体の体積(2) 直方体の横の長さと体積の関係 いろいろな体積の単位 いろいろな単位・およその単位単位胞の選び方-規則2 結晶軸は常に3つの相互に直交す 無 る2回又は4回回転軸とにとり、4つ の3回回転(回反)軸は立方体の体 対角線と平行にする 立方 三方晶系では3 回回転軸は単純単位 格子の体対角線方向に沿ってとり、 a=b=c、α=β=γ≠90ºとする
30/5/21 二等辺三角形を利用する問題です。角度の問題ですが、角度だけでなく、長さも考えなくてはいけません。角度の問題が苦手な子どもは、この段階でつまづいている場合が多いです。 ★★★ download 角度9 おうぎ形の折り返し 説明15/8/ 空間図形 立方体を切断したときの切り口の考え方 中学数学 定期テスト対策 空間図形 立方体を切断したときの切り口の考え方 「立方体において,3点を通る平面で切った場合の切り口がどうなるか」という問題がありますが,どのように考えればいいのかわかりません。面積のもとめ方の工夫c 解説 面積のもとめ方の工夫d 解説 まわりの長さ 解説 面積の求め方(ブロック地図) 解説 面積の求め方(ブロック図形) 解説 角とその大きさ 分度器 解説 分度器ペンつき 解説 分度器角度扇の色つき 解説 2度の測り方 解説 340度の測り方



5年算数体積2わかる教え方




三角錐 四面体 の体積の公式 Schoolmath S Diary
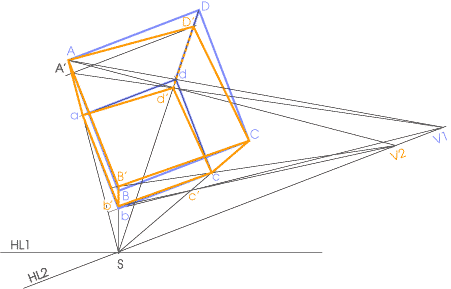
図で青線で描かれているのは平行透視で立方体を表している。 CDと視点Sからの垂線との交点をPとし、立方体の底面の各頂点ABEFとを結ぶ。 Cから任意の角度で斜線を下ろし、PBとの交点をqを求める。 この点の求め方には取り決めがないので、斜線の角度を求めるにはある程度のデッサン力も必要になる。 qから水平線をのばしrを求める。 q、rと視点Sとを結び作図を⑴ 三角錐の体積を求めなさい。 〔 〕 ⑵ bcdを底面としたときの三角錐の高さを求めなさい。 〔 〕 8 右の図のように,1辺が6cmの立方体abcdefghがある。この立方体 の3つの頂点a,b,gを結んでできる abgについて,次の問いに答えな さい。 (秋田)問1:ABとCGのなす角度を求めなさい まずは、ABとCGのなす角度です。 この2つの辺は接していないのでなす角度がないと思われるかもしれませんが、この手の問題は ABをDCに平行移動して 考えてみましょう。 ABとCGのなす角度ということは、DCとCGのなす角度と同じということです。 ∠DCG=90°なので、ABとCGのなす角は「90°」が答えとなります。



心に強く訴える 立方体 と 直方体




問題174 立方体に潜む正多角形
課題学習の指導(数学) 1.はじめに 「ひもで立体の表面上の頂点と頂点とを結び,その長さを調べてみよう。 」 このような課題は,3年の「三平方の定理の利用」でとりあげられることが多い。 しかし,1,2年までの空間図形や平面図形の見方・考え教え方4-① 大きな直方体や立方体の体積を計算して求める方法に気づかせ、 (立方メートル)の単位を教えます。 問題 下図の直方体の体積を求めましょう 直方体の体積は、たて×横×高さで求められるので、cmで表すと 300cm×400cm×0cm = となります。ちょっと難しい言い方をすると 同じ平面上にない と言うこともできます。 ねじれの位置の見つけ方 それでは問題を使って、ねじれの位置を見つける練習をしていましょう。 次の直方体において、辺aeとねじれの位置にある辺を見つけましょう。
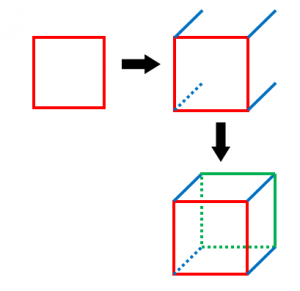



立方体と直方体の見取り図の書き方 具体例で学ぶ数学



斜視図 等角図 の描き方 小山特許事務所
立方 なし 1本のc2 3本の直交c2 1本のc3 1本のc4 1本のc6 正四面体配置 の4本のc3 12 図・5立方晶系に属する単位胞には,正四面体的に配列した4本 の3回回転軸がある.3回軸をC3で表す.挿入図は3回対称を表す. この不思議な図形は人 の"目"です.立方体の 簡単公式台形の体積(正四角錐台)の求め方がわかる3ステップ 台形の体積の公式の求め方を知りたい!? こんにちは!この記事をかいているKenだよ。着る毛布ほしいね。 台形の体積の求め方 を教えてほしい。 そう、きかれることが結構ある。 正直無料授業動画サイト「StudyDoctor」 http//studydoctorjp/家庭教師テキスト http//studydoctorjp/?page_id=4英語はmiki先生 https//www
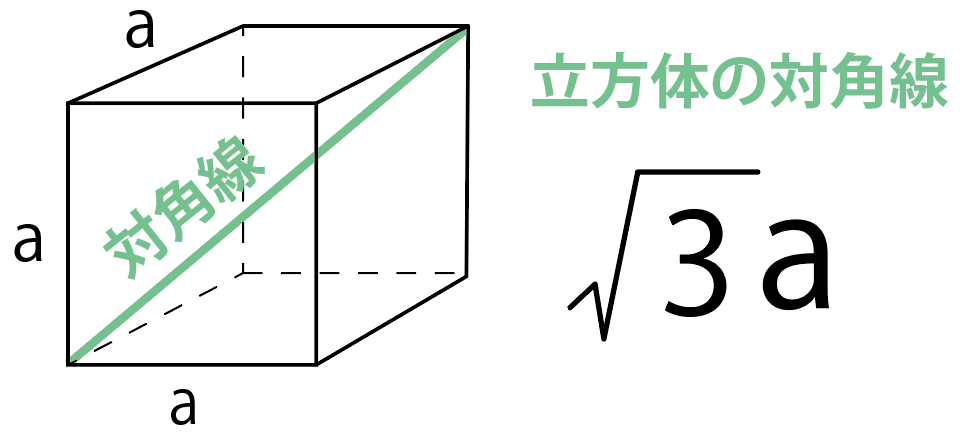



計算公式 立方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
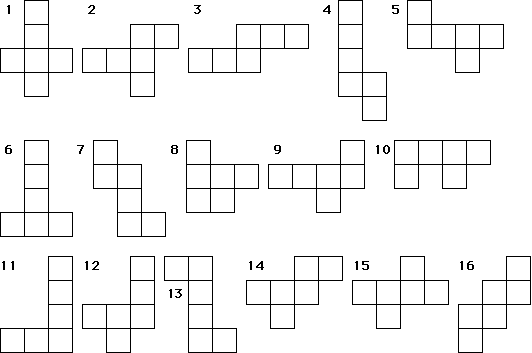



イメージが苦手でも解ける 立方体の展開図 算数の教え上手 学びの場 Com
第144問 直方体の角度 図形ドリル 6年生 正三角形 直方体 立方体 角度 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を体心立方格子の場合 原子位置 = 2 ( h k l = 偶数 ) 0 ( h k l = 奇数 ) (001) 間に格子面があり、この面での反 射による干渉で消える (110) 間に格子面が無いのでブラッ グ反射がそのまま適用できる 慣用単位胞で考えたための問題、基本単位胞をとればおこらない28/1/21 ここでは、直径2cmの球を描こうとしていますから、直径が244cm(2×122)の円を描きます。 等角図は、物体を斜め上方から見た図となります。 この場合、前記 立方体 の各辺の寸法などは、本来は実寸よりも小さく(つまり等角図ではなく等角投影図のよう




3 なす角135 の意味がわからない Clear




中学数学 空間図形
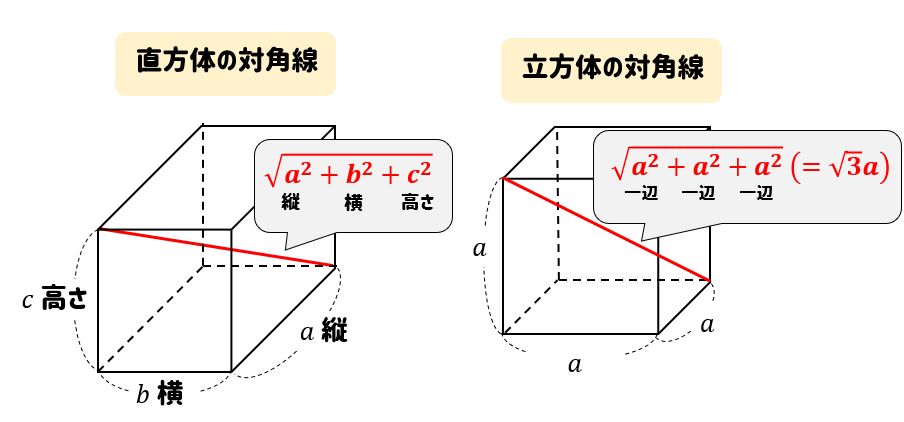
立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)底面積の求め方は?5分でわかる計算、円柱、円錐、四角柱、三角柱の底面積 立方体の底面積 立方体は全ての辺が同じ長さです。よって底面の面積は「正方形の面積」を求めればよいですね。立方体の底面積は下記の通りです。 立方体の底面積=5×5=25cm 2直方体の対角線の長さ たて、横、高さがそれぞれ、 a,b,c a, b, c である直方体の対角線の長さを L L とすると、 L = √a2 b2 c2 L = a 2 b 2 c 2 三平方の定理の斜辺の長さと似ていますね。 「三平方の定理の立体版」って感じがしますね。



Another Pars Page
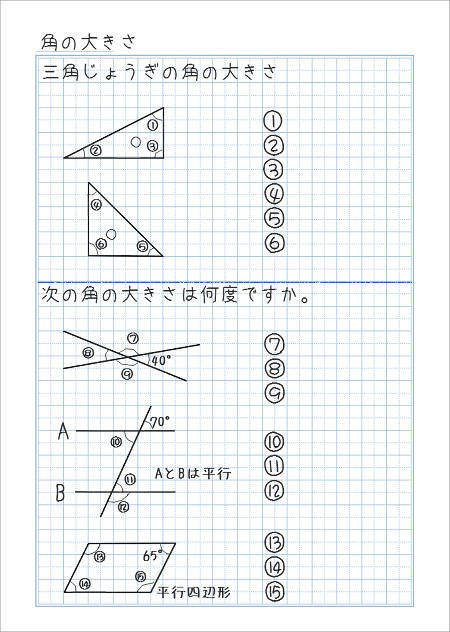



角の大きさを計算で求める自主学習ノート例 家庭学習レシピ
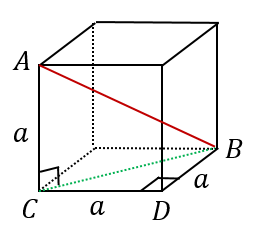
θ = ∠ A G B \theta=\angle AGB θ = ∠AGB は, cos θ = − 1 3 \cos\theta=\dfrac {1} {3} cosθ = −31 を満たす。 具体的には, θ ≒ 109 5 ∘ \theta\fallingdotseq 1095^ {\circ} θ ≒ 1095∘長方形の対角線の長さの求め方のまとめ 対角線の長さは、 三平方の定理 を使って求める 対角線の長さ = √a2 b2 = a 2 b 2 スポンサーリンク スポンサーリンク 正方形の対角線の長さの求め方 ←BACK NEXT→ 平行四辺形の対角線の長さの求め方 おすすめ11/5/19 こちらも上の公式を基に計算していきましょう。 なお、イメージしにくいときは、上のよう立体図形を実際に書いてみるといいです。 そして立方体の対角線の長さは√3× 6 = 1732 × 6 = と算出されるのです。 なお、この公式自体を忘れたとしても、導出できるようにしておくといいです。 詳しい手順を以下で確認してます。 まずは、底面の対角線




高校数学 正四面体の計量 表面積 2面のなす角 高さ 体積 内接球の半径 外接球の半径と立方体への埋め込み 受験の月




立方体の あの角度 フィボナッチ フリーク
5/8/09 対角線と辺を含む直角三角形(辺と対角線の共通交点と反対側の交点を結ぶ面の対角線でできる三角形)を作ると直角を挟む辺の比が1:√2 なので 三平方の定理から3辺の比は 1√2:√3が求まります。 tanθ=√2/1 なので θ=arctan (√2)≒ rad≒5474°直方体、立方体の対角線を求めるには、 次のように2つの三角形に分けるて考えていきます。 すると、赤い直角三角形に注目すると 求めたい対角線 の長さは次のように表すことができます。 でも 上記にも書いた通り、 『立方体は、正方形6枚が組み立てられて出来ているため、 全ての辺は同じ長さであり、「平行な関係や垂直な関係」が 多数見られる図形である』 よって、beと共に角をなし、なおかつghと「平行や垂直」の 関係にある「代わりとなる辺」を探そう。




体積の求め方 計算公式一覧



Www Nichibun G Co Jp Textbooks Sansu Download R2 R2 Sansu Digitb Guide Pdf
変形立方体(へんけいりっぽうたい、英 snub cube 、ねじれ立方体、ねじり立方体)または変形立方八面体(英 snub cuboctahedron )とは、半正多面体の一種であり、正六面体の面をねじり、間に正三角形を入れたような立体である。 カイラルであり、ねじる方向により違いが現れる。 展開図(直方体・立方体)のポイント 重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士 立方体の「最も遠い点」展開図の長方形( 2つ)の対角線にくる 平行な辺は立体図でも展開図でも平行 立体図で平行な面は展開図で1つ飛ばしになる



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



5年算数体積2わかる教え方
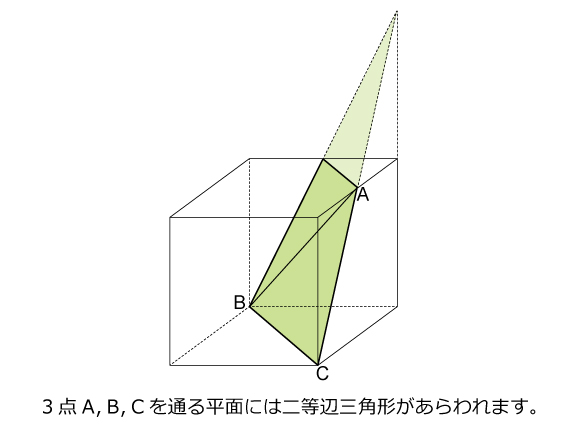



図形ドリル 第243問 立方体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦
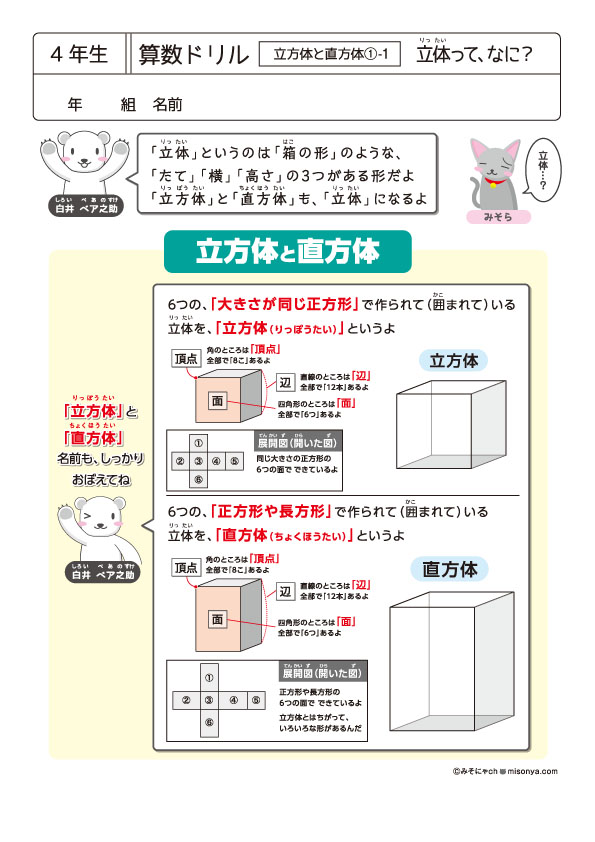



無料の学習プリント 小学4年生の算数ドリル 立方体と直方体1 みそにゃch




空間図形の基本 体を空間に慣らしましょう 数学b By Okボーイ マナペディア




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




立方体の切断 に関するまとめをアップしました お見逃しなく 恋する中高一貫校 適性検査 中高一貫校徹底攻略 中学数学 小学校 算数 中学受験



角度計算 ツール パースフリークス



星型の角度の求め方 算数解法の極意
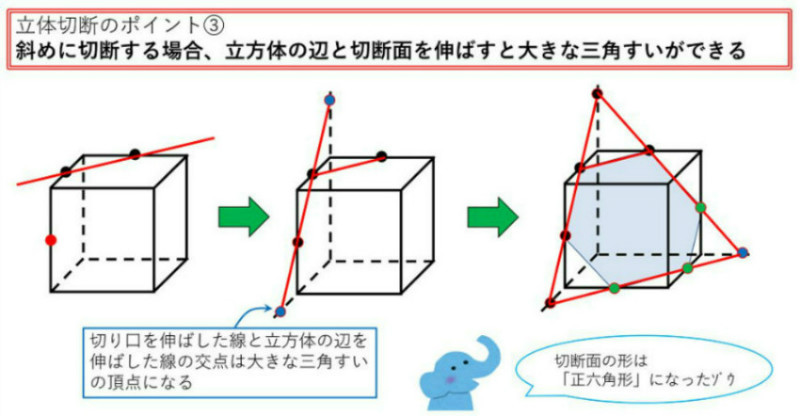



講義内容3




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



数学の質問です 画像の図の立方体において 直線beとghのなす角の求め方 Yahoo 知恵袋




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり
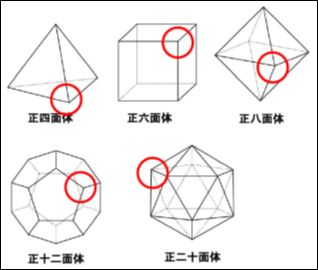



正多面体は5種類しかない 2 Only 5 Kinds Of Regular Polyhedron 2 同志社中学校
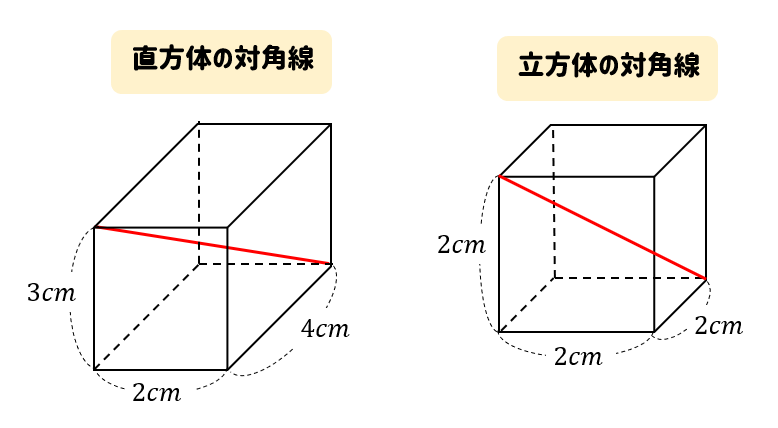



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



1



Studydoctor立方体と空間ベクトルの内積 数b Studydoctor




算数 積み上げた立方体の個数 なるほどの素
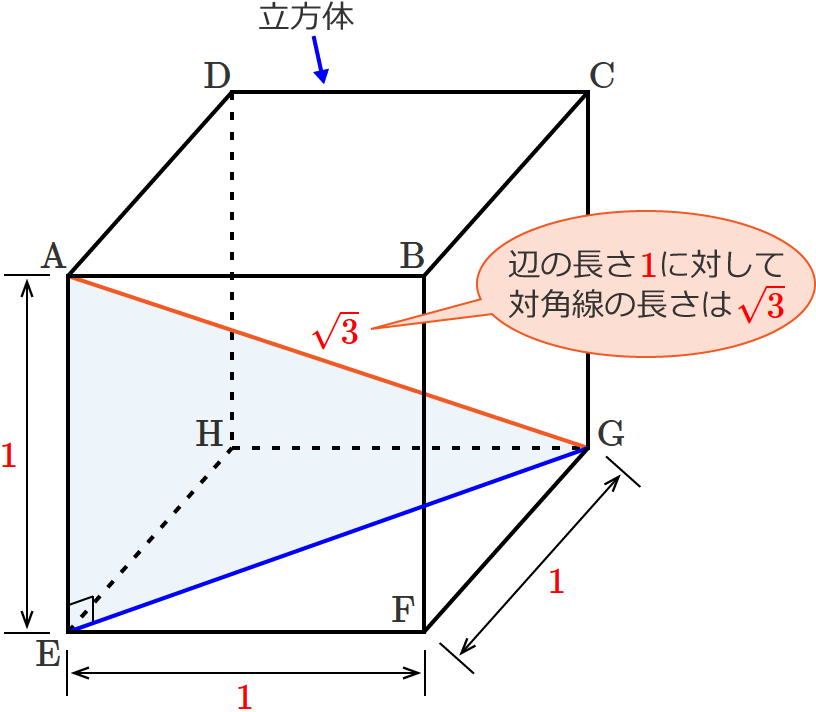



立方体の対角線の長さの求め方




立方体と直方体の面 辺 頂点 Youtube



立方体の描き方 2点透視 パースフリークス
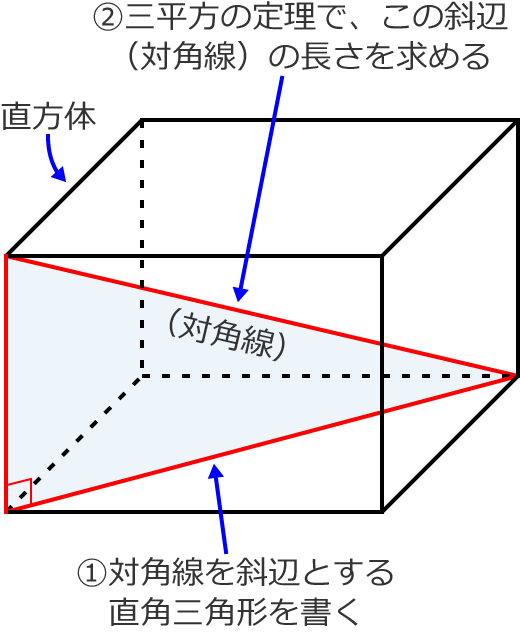



直方体の対角線の長さの求め方
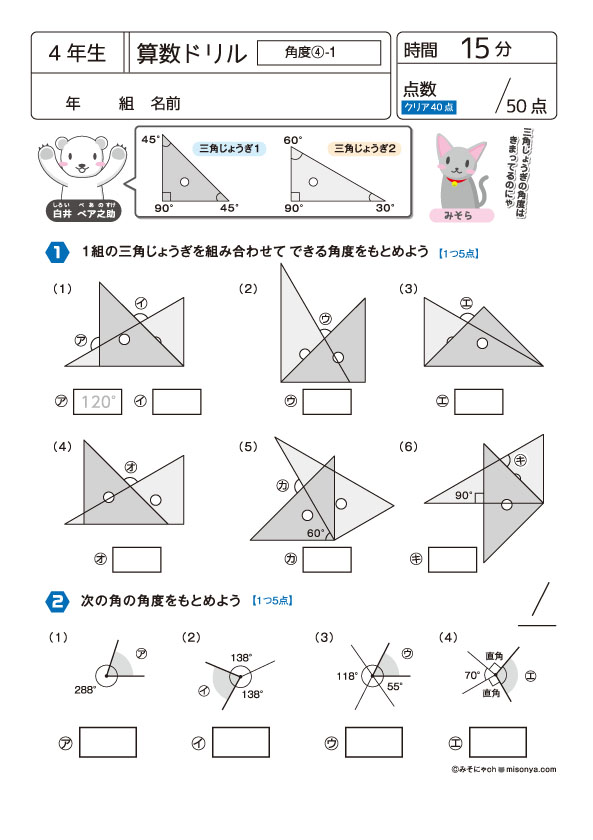



無料の学習プリント 小学4年生の算数ドリル 角度4 総合問題 みそにゃch




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




上 図形 角度 求め方




数学 台形 角度の問題教えて 添付の台形 Dの角度が1 になる理由 数学 教えて Goo




この問題の二等分された部分の と の1つの角の大きさの求め方を教えてください ち Clear




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ
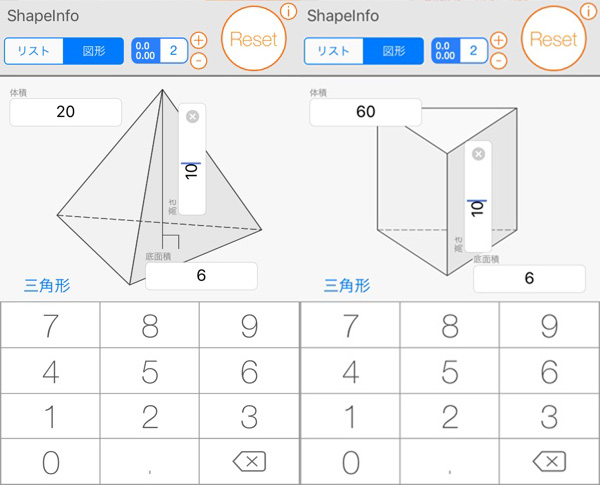



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 Isuta イスタ 私の 好き にウソをつかない




体積 直方体 立方体 5 算数 算数 問題 算術



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



立方体の対角線の長さの求め方




角cafの大きさを教えてください 1辺が3の立方体です 私は角cab 45 その他 学校 勉強 教えて Goo




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント
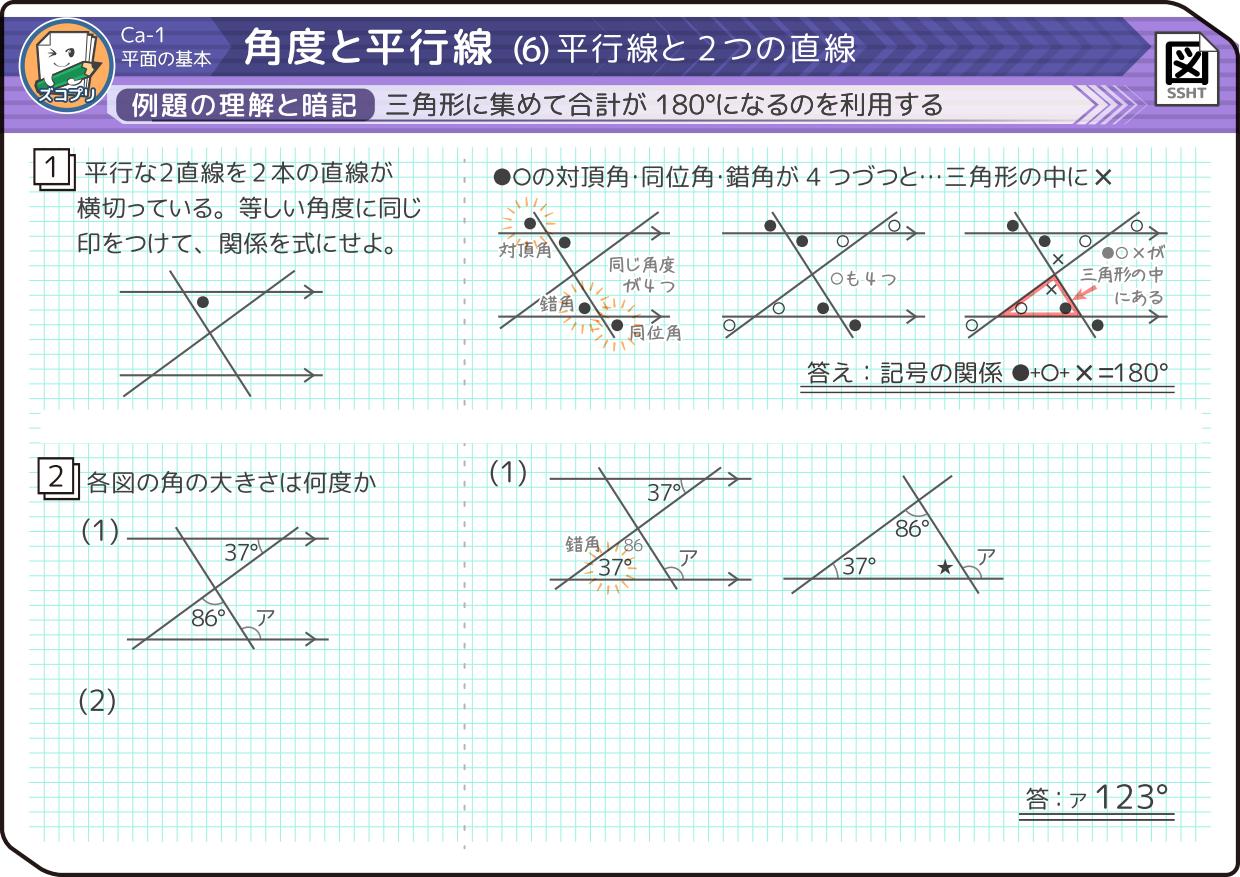



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
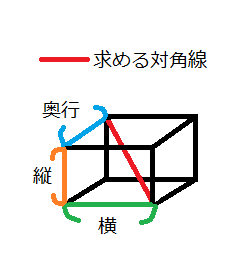



直方体の対角線の長さ 高精度計算サイト




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




ぬるいパースが描けるようになりたい 09年03月
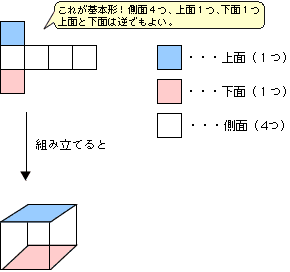



イメージが苦手でも解ける 立方体の展開図 算数の教え上手 学びの場 Com



2




高校数学a 2直線のなす角 例題編 映像授業のtry It トライイット
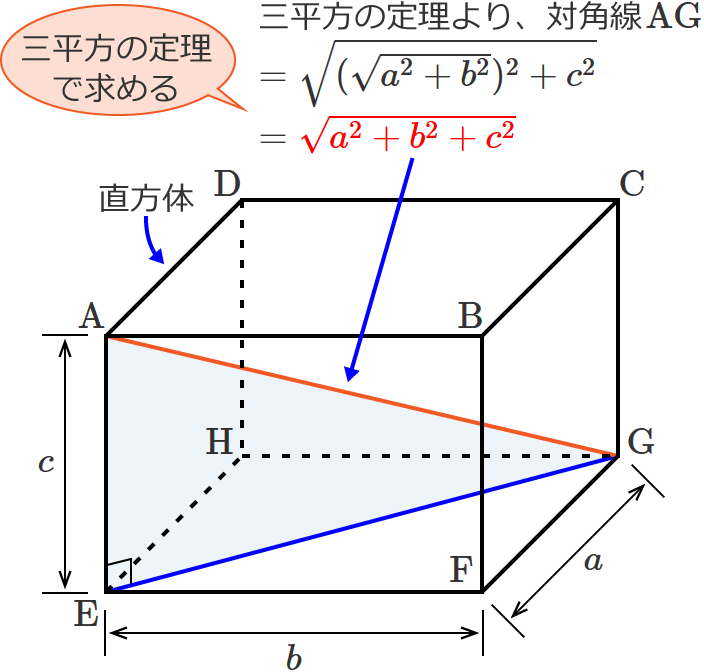



直方体の対角線の長さの求め方



この問題の解き方教えてください 図は立方体の見取り図です Yahoo 知恵袋



大至急教えてください 下図の立方体の三角形aegの角度と 各面とこの三角形ae Yahoo 知恵袋




吉田誠治 パソコンのモニターも三点透視ですね また背もたれについては以下の図のような理論で消失点を求め られます なお 図の消失点 の求め方は更に厄介なので専門書をご覧ください とりあえず地平線上になんとなく置いて いろいろ試してみるのが良い




ルパート王子の立方体 Wikipedia




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



立方体の中にある三角すい 算数解法の極意
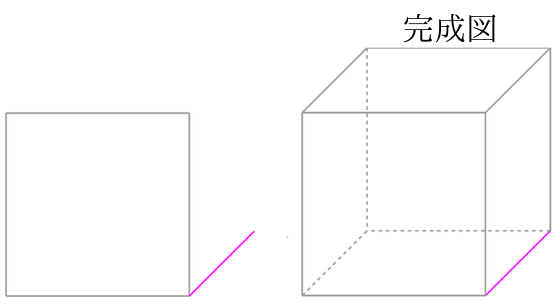



数学の空間図形で必要な直方体や立方体等の図形の描き方は 立体を簡単に描くコツとは さびねこ中学校




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり



1



立方体の切断についてこの画像の立方体の切断面の角度は 90度 Yahoo 知恵袋



1
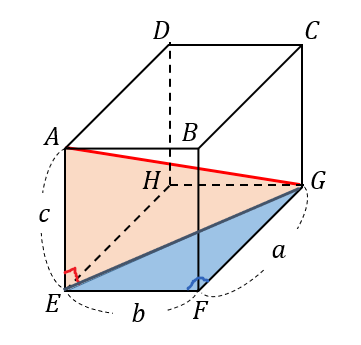



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



Http Www Ikushin Co Jp Shuppan Textimg 17matokan Chuhyo Sugaku Hon Pdf
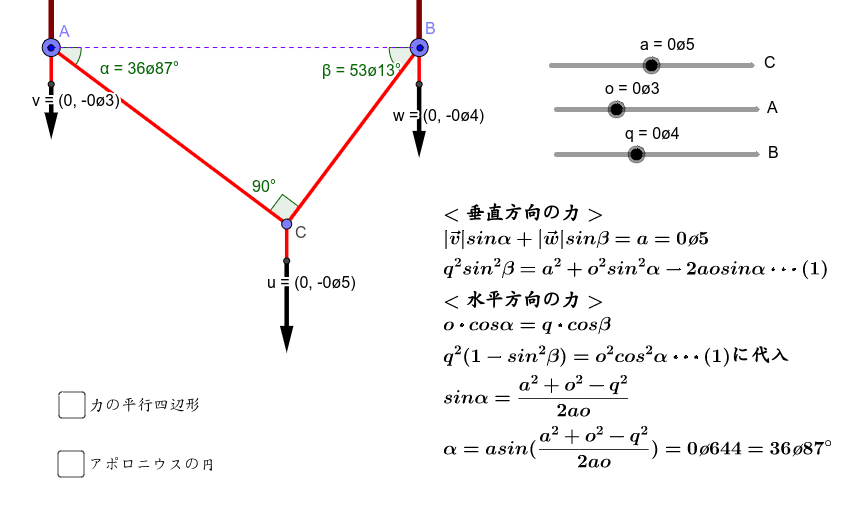



力の平行四辺形の角度の求め方 Geogebra




空間図形に含まれる三角形の面積を求める問題 直方体 数学i By ふぇるまー マナペディア



立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
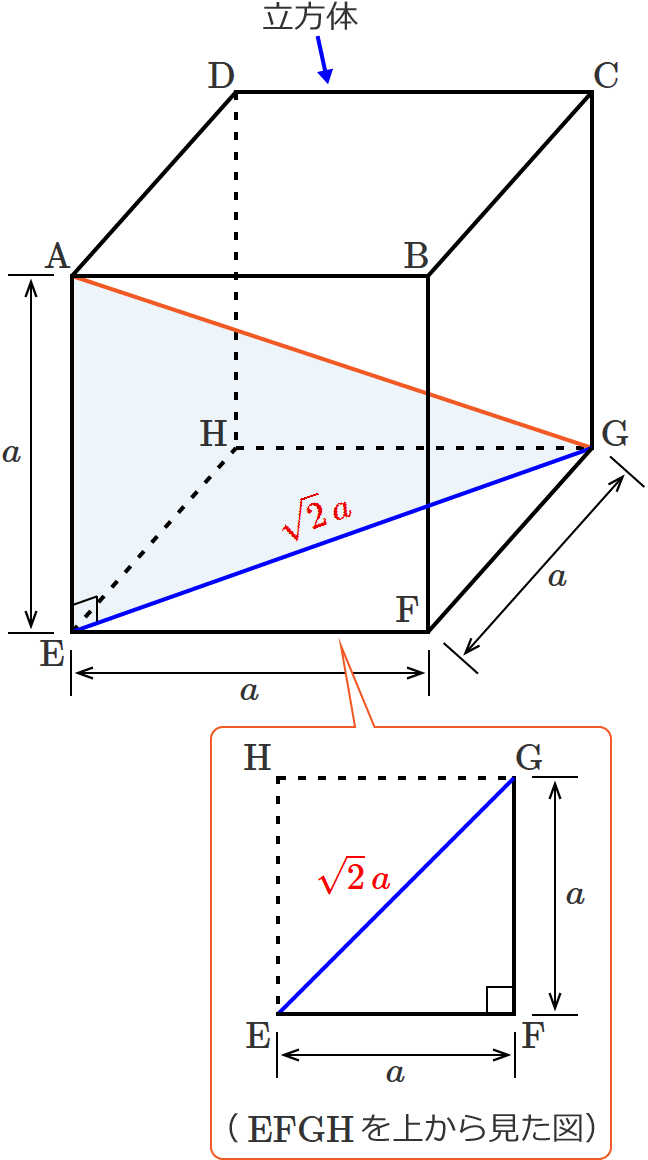



立方体の対角線の長さの求め方
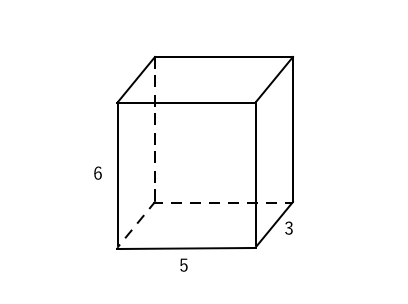



超簡単 体積の求め方 苦手な数学を簡単に




角cafの大きさを教えてください 1辺が3の立方体です 私は角cab 45 その他 学校 勉強 教えて Goo
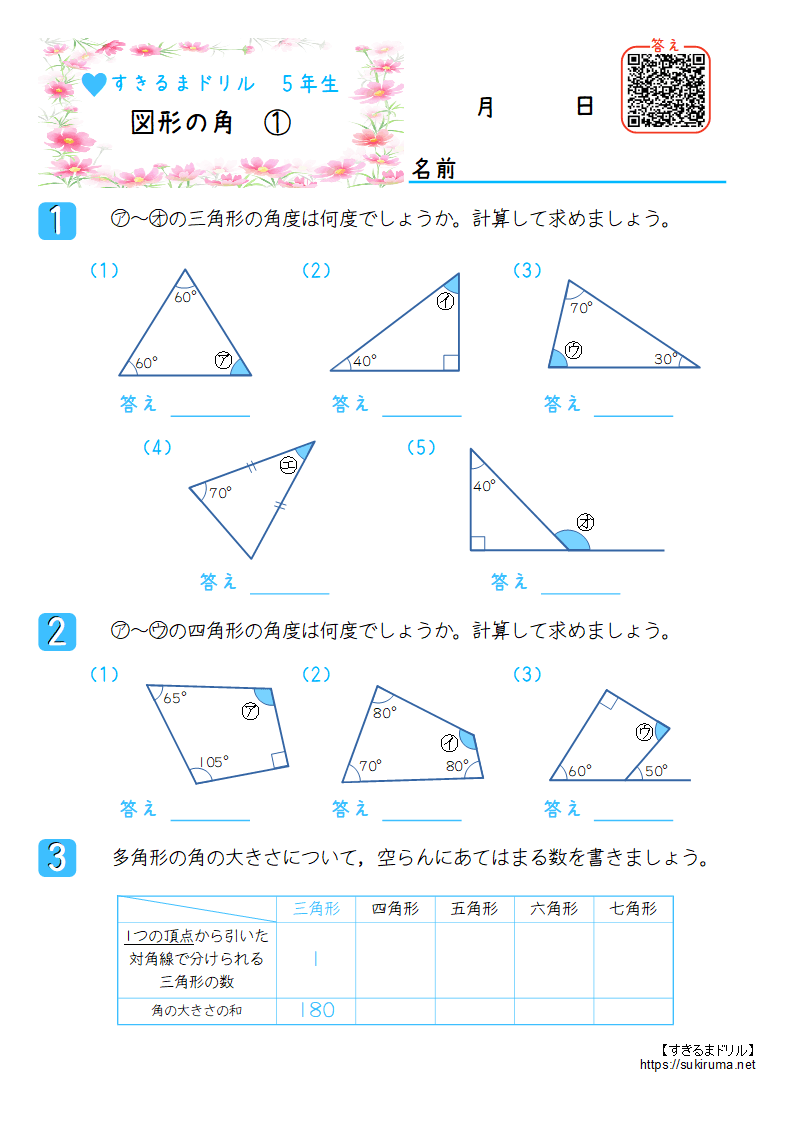



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント




計算公式 直方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直線と平面の位置関係 平行 垂直 ねじれの位置 数学fun




Cube Taraognn
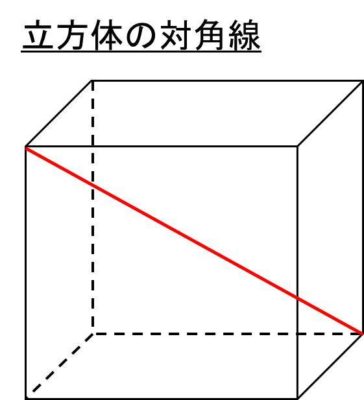



立方体の対角線の計算方法 白丸くん
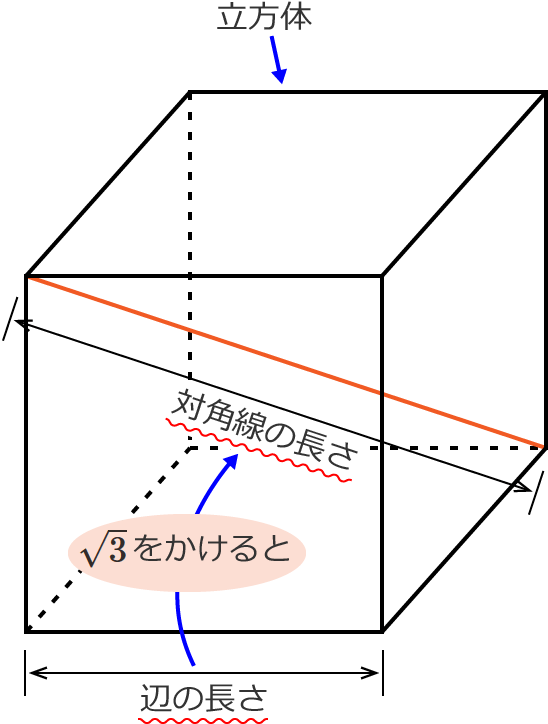



立方体の対角線の長さの求め方




基本 立方体と空間ベクトルの内積 空間ベクトル3 01 Youtube




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス
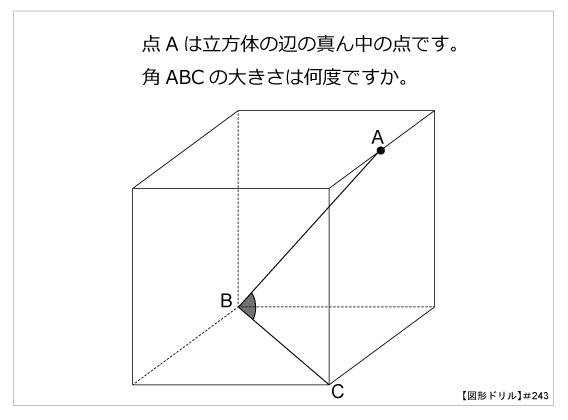



図形ドリル 第243問 立方体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦



立方体と直方体の対角線の長さ 具体例で学ぶ数学




ぬるいパースが描けるようになりたい 立方体をいろんなアングルから 平行投影 もう少し細かいバージョン
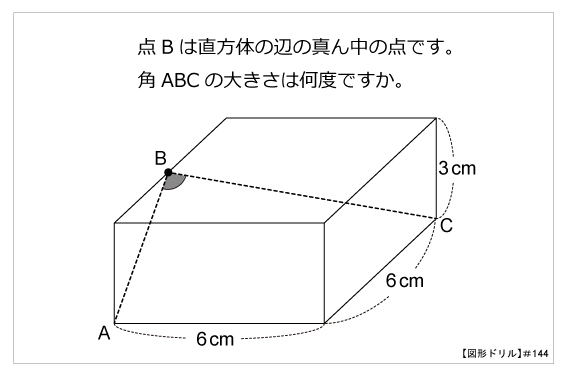



図形ドリル 第144問 直方体の角度 算数星人のweb問題集 中学受験算数の問題に挑戦



立方体と直方体の対角線の長さ 具体例で学ぶ数学




ルパート王子の立方体 Wikipedia



バカでもわかる 中学数学




余弦定理で角度を求める方法 数学の星




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



1



1辺aの正四面体の長さ 面積 体積 2平面のなす角度などまとめ 数学の偏差値を上げて合格を目指す




5年生 三角形 角度の求め方 Youtube




立方体の対角線の角度を求める問題 恋する中高一貫校 適性検査 徹底攻略
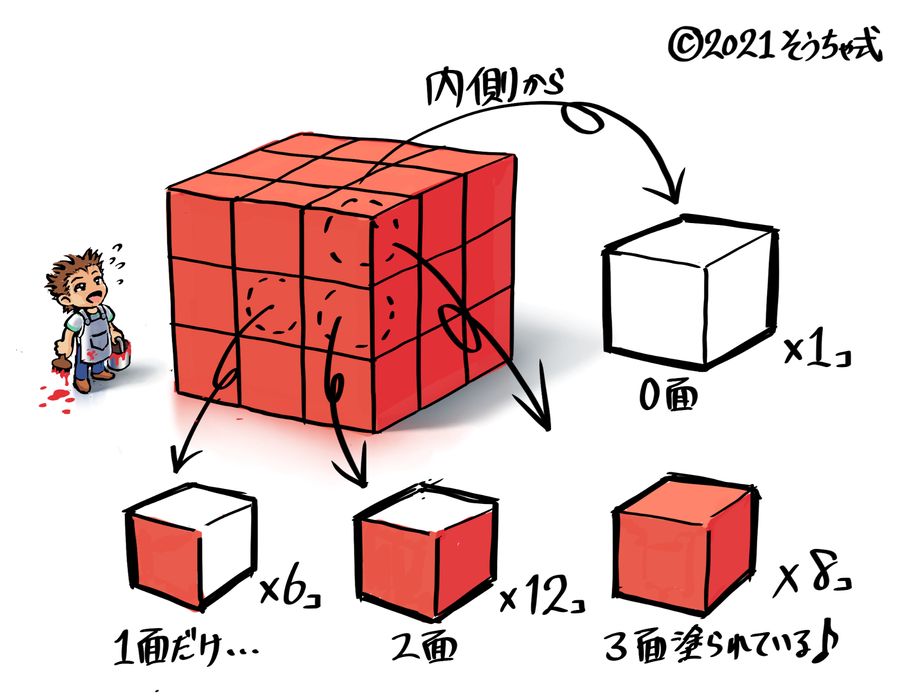



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ




上 図形 角度 求め方



立方体の描き方 2点透視 パースフリークス



折り返し角度問題のポイントはこれ 算数解法の極意



0 件のコメント:
コメントを投稿